All are welcome at the Symposium on Geometry Processing 2022.
Attendees, presenters, volunteers and sponsors are subject to the SGP
2022 Code of Conduct.

Keynotes

Angela Dai
Technical University of Munich
Towards Structured Geometric Understanding for 3D Perception
Semantic perception of 3D environments has seen remarkable advances in recent years, with a significant focus on object-based understanding. We propose to learn structured, intermediary representations, such as object parts, in order to provide a robust understanding of diverse 3D geometric structures from observations of real-world environments. This can enable more effective geometric reconstruction of objects in 3D scenes, enabling inter- and intra-object reasoning, as well as establish efficient structured representations for reconstruction and tracking of objects undergoing complex deformations.

Ligang Liu
University of Science and Technology of China
Computational 3D Visual Art Design
3D visual arts are highly diverse, including sculpture, architecture, ceramics, etc., in our lives. Traditionally, artists use their rich imagination and experience to design 3D objects to give the audience a memorable experience. The design process takes a lot of trial and error, so it is often very time-consuming. It has attracted the attention of many researchers in the community of geometry processing and computer graphics, proposing various algorithms to simplify the initial complicated design process and help artists quickly realize the art in their minds. Moreover, the advent of digital modeling and 3D printing enables artists to create more complex 3D visual artworks. In this talk, we will show a few interesting 3D visual art works and propose automatic methods to solve various problems in the design process of these art works. From these examples, we reveal the close connection between geometry processing techniques and various 3D visual art design problems. Moreover, we will discuss about the current research trends and provide an outlook for future research directions and solutions.

Caitlin Mueller
MIT Architecture
Geometry for design and construction of high-performance architecture
Design and construction in the built environment present significant challenges and opportunities for impact: Buildings contribute to about 40% of global carbon emissions through their materials and operations, often due to inefficiencies stemming from a lack of integration between architectural design, engineering, and construction processes. While this disconnect has been critiqued for decades, today's emerging techniques in computation, and in particular, geometry, can allow for a new layer of interdisciplinary communication and collaboration that transforms traditional workflows and empowers novel visual languages for high-performance architecture. In this talk, Mueller will share recent work that contributes to this goal, demonstrating new techniques for computational design that integrate engineering principles and sustainability goals without overriding creative autonomy, and new fabrication methods that can materialize efficient geometries economically. In particular, the talk will demonstrate how techniques developed in geometry processing and related fields can empower significant innovation in architectural domains, and will propose emerging problem spaces and applications for future geometry research.

Daniele Panozzo
New York University
Robust Geometry Processing for Physical Simulation
The numerical solution of partial differential equations (PDE) is ubiquitously used for physical simulation in scientific computing, computer graphics, and engineering. Ideally, a PDE solver should be opaque: the user provides as input the domain boundary, boundary conditions, and the governing equations, and the code returns an evaluator that can compute the value of the solution at any point of the input domain. This is surprisingly far from being the case for all existing open-source or commercial software, despite the research efforts in this direction and the large academic and industrial interest. To a large extent, this is due to lack of robustness and generality in the geometry processing algorithms used to convert raw geometrical data into a format suitable for a PDE solver. I will discuss the limitations of the current state of the art, and present a proposal for an integrated pipeline, considering data acquisition, meshing, basis design, and numerical optimization as a single challenge, where tradeoffs can be made between different phases to increase automation and efficiency. I will demonstrate that this integrated approach offers many advantages, while opening exciting new geometry processing challenges, and that a fully opaque meshing and analysis solution is already possible for heat transfer and elasticity problems with contact. I will present a set of applications enabled by this approach in reinforcement learning for robotics, force measurements in biology, shape design in mechanical engineering, stress estimation in biomechanics, and simulation of deformable objects in graphics.
Graduate School
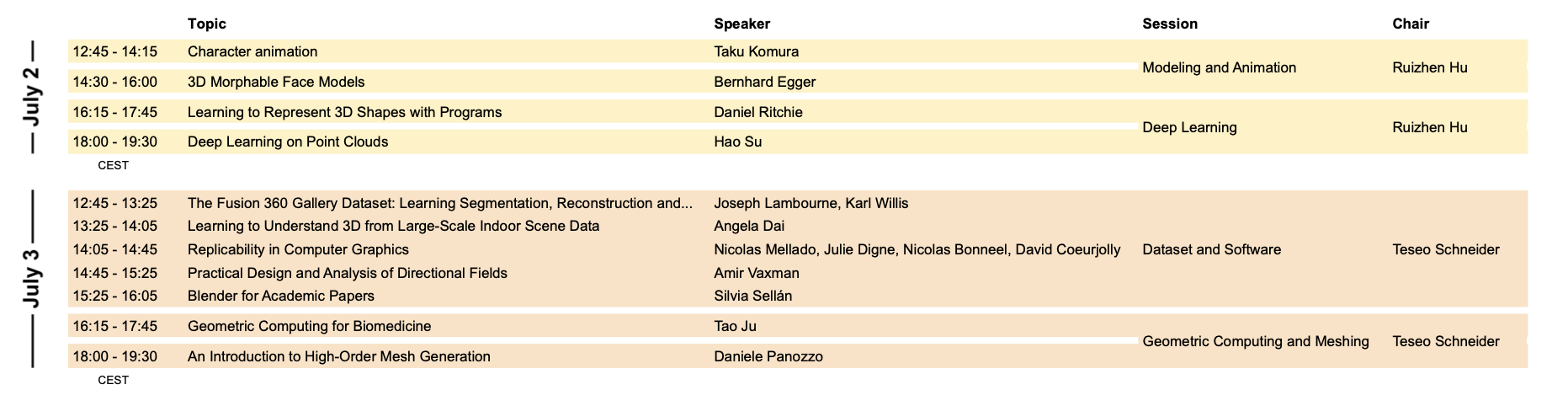
Note that all the graduate school lectures will be recorded for later access.
Deep Learning on Point Clouds

- Hao Su, UC San Diego
Point cloud is an important type of geometric data structure. They are simple and unified structures that avoid the combinatorial irregularities and complexities of meshes. These properties make point clouds widely used for 3D reconstruction or visual understanding applications, such as AR, autonomous driving, and robotics. This course will teach how we apply deep learning methods to point cloud data. We will cover the following topics in this short course and will end with some open problems.
- • Basic neural architectures to process point cloud as input or to generate point cloud as output
- • Scene-level understanding of static and dynamic point clouds
- • Point cloud based inverse graphics
- • Learning to convert point cloud to other 3D representations
- • Learning to map point cloud with data in other modalities (images, languages)
Learning to Represent 3D Shapes with Programs

- Daniel Ritchie, Brown University
There are many representations for 3D shapes: triangle meshes, point clouds, parametric surfaces, signed distance fields, and so on. Different representations may be better for certain tasks: acquisition, editing, rendering, etc. In recent years, the space of possible 3D shape representations has been a topic of much discussion because of a new task: machine learning. Specifically, researchers have been exploring the following question: which 3D shape representations are best for learning from data? In this course, we’ll discuss a 3D shape representation with an old history that has been receiving renewed attention in today’s learning-based era: programs. Programs (i.e. executable symbolic descriptions of a structure) have several properties that make them attractive for learning. For example, they can be constructed such that they cannot represent certain undesirable geometric artifacts that often plague learning-based systems, and their discrete symbolic nature makes them well-suited for processing with powerful neural language models such as Transformers. Specifically, this course will cover the following, and we’ll conclude with some thoughts on current open problems in this field as well as ideas for new graduate students to pursue.
- • Learning problems/tasks involving program representations (visual program induction, generative modeling)
- • Domain-specific languages (DSLs) for shape modeling: current popular choices and considerations to make when choosing/designing one for your own project
- • Machine learning model architectures for learning/processing program representations
- • Algorithms for supervised and unsupervised learning of program representations for 3D shapes
3D Morphable Face Models

- Bernhard Egger, Friedrich-Alexander-University, Erlangen-Nürnberg
A 3D Morphable Model (3DMM) is a statistical object model separating shape from appearance variation. Typically, 3DMMs are used as a statistical prior in computer graphics and vision. A model is learned from high-quality 3D scans of multiple object instances. It reduces the dimensionality and provides a low-dimensional, parametric object representation. The resulting model is generative, which means that from a set of randomly sampled parameters a novel realistic object instance arises. Such a model can then be used in various settings, we will focus on the inverse rendering setting, where we try to reconstruct the 3D face from a 2D image with the 3DMM as prior. In this tutorial I will introduce 3DMMs from scratch and focus on explaining every single component behind a 3DMM. We will also have a short outlook at various applications and how 3DMMs are used today and combined with other modeling techniques.
Character animation

- Taku Komura, University of Hong Kong
Character animation is a topic that has a wide range of applications for films, computer games, digital entertainment, automatic driving, Metaverse and virtual reality. In this lecture, I will start from the basics of character animation and then discuss novel topics in facial animation, data-driven full body motion synthesis based on neural networks, reinforcement learning and physically-based animation.
Geometric Computing for Biomedicine

- Tao Ju, Washington University in St. Louis
With the advance of biomedical imaging technology, research in biology and medicine increasingly relies on the ability to robustly and efficiently extract knowledge from raw images. The goal of this course is to offer an overview of the roles that geometry processing can play in this data-to-knowledge process. The course starts with a brief introduction to biomedical imaging and the typical computational tasks on these images (e.g., segmentation, analysis, registration, etc.). The bulk of the course will be devoted to several examples of geometry processing problems that arise from accomplishing these tasks, including meshing of scalar fields, slice-based surface reconstruction, topology simplification, and skeletonization, and progress made so far for solving each problem. The course will end with a few example biomedical applications that utilize geometry processing algorithms.
An Introduction to High-Order Mesh Generation

- Daniele Panozzo, NYU
Meshes with curved edges are a useful discretization to represent curved geometries or high-order displacement fields more compactly than their linear counterpart. The smaller number of degrees of freedom, coupled with the additional flexibility in the shape of the elements, has major computational advantages. However, the curved geometry introduces additional algorithmic and numerical challenges. In this lecture, we discuss the advantages and disadvantages of linear and curved meshes and overview the current state of the art in both curved mesh generation and their use for the solution of partial differential equations with the finite element method. A particular focus is on the major open geometric challenges introduced by the curved boundaries, including checking for inversions, Boolean operations, collision detection, and input sanitization for the commonly used SVG and STEP industrial standards. The prerequisites for this lecture are an undergraduate linear algebra course and an undergraduate graphics or geometry processing course. A course on numerical methods and/or on the finite element method is a plus but not necessary.
The Fusion 360 Gallery Dataset: Learning segmentation, reconstruction and assembly modeling

- Joseph Lambourne, Autodesk
- Karl Willis, Autodesk, London
Almost every manufactured object in the world around us starts life as a computer-aided design (CAD) model. Industrial CAD models contain rich, multi-faceted data describing precise geometry as analytical surfaces, complex topology for parts as well as assemblies, and the underlying sequential modeling operations invoked by the CAD user. This talk introduces the Fusion 360 Gallery Dataset, a collection of CAD data submitted by users to the Autodesk Online Gallery. We give an overview of the available data and present some of our recent research which utilizes this for segmentation, CAD sequence determination and assembly modeling. We also outline unsolved challenges and areas for future investigation.
Learning to Understand 3D from Large-Scale Indoor Scene Data

- Angela Dai, Technical University of Munich
We have seen a revolution in 2D image understanding, driven by large-scale image datasets coupled with advances in deep learning. How can we bring this to 3D perception, which is fundamental to understanding scene structure to enable higher-level understanding such as interaction with environments? This talk will discuss the creation of large-scale 3D annotated datasets to enable learning strong data-driven priors, with focus on the ScanNet dataset. We will additionally discuss open challenges with existing 3D data, learning efficiently in limited data scenarios, and under potentially imperfect data.
Replicability in Computer Graphics

- Nicolas Mellado, CNRS - IRIT
- Julie Digne, CNRS - LIRIS
- Nicolas Bonneel, CNRS
- David Coeurjolly, CNRS - LIRIS
In this talk, we will introduce the concept of replicability, and its benefits in research. We will present how replicability affects the work of researchers, the visibility of the research outcomes, and the impact on their diffusion. We will also cover the tools that are today available to develop replicable research, and attempt to sketch guidelines and best practices for research practitioners, e.g., students, researchers.
Practical Design and Analysis of Directional Fields.

- Amir Vaxman, Utrecht University
Directional fields on surfaces and in volumes are important features of geometry processing. Such fields can represent flows, alignments, or trends in geometry. In this tutorial, we will learn some of the elementary building blocks of directional field processing. Namely, we will demonstrate how to build discrete consistent representations, connections, and differential operators. Finally, we will talk about field visualization. These constructions will be represented using examples from Directional (https://github.com/avaxman/Directional).
Blender for Academic Papers

- Silvia Sellán, University of Toronto
There are a lot of great Blender tutorials online, and they are usually aimed at artists or animators who want to generate full scenes from scratch for short films. They go into depth on how to model a shape, how to pick the best lighting, how to design a material, create textures, etc. These can be overwhelming if you are an academic and all you want is to render your object beautifully for a SIGGRAPH paper figure. This can lead to a lot of frustration especially near deadlines, when one does not have the time or energy to learn a whole new aspect of the software just for a minor change in a paper figure. In this course, aimed at absolute Blender beginners, we will mitigate this frustration by walking slowly from .obj file to beautiful paper figure, showing tricks to save time and effort.
Technical Papers
Proceedings (accessible from July 4th)
MODELING & MAPPING chaired by Mirela Ben-Chen
|
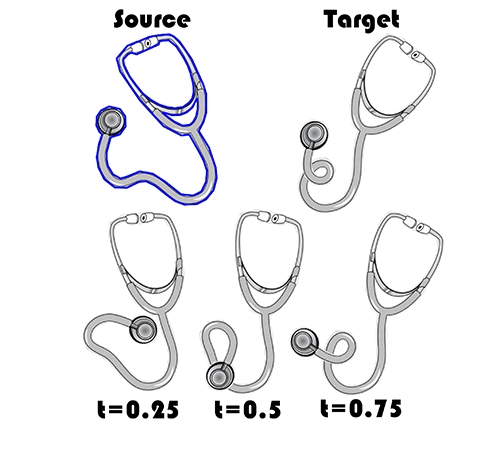
Harmonic Shape Interpolation on Multiply-connected Domains |

|
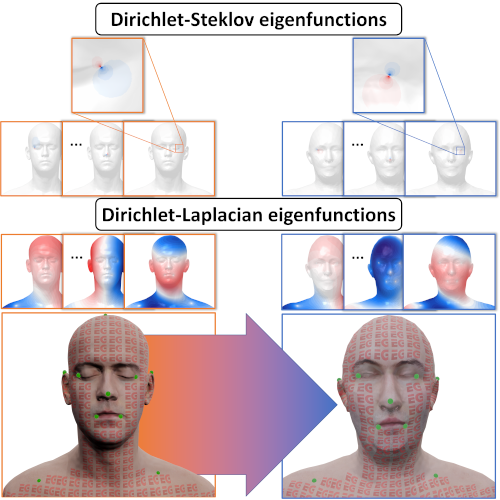
Localized Shape Modelling with Global Coherence: An Inverse Spectral Approach |
|
Non-Isometric Shape Matching via Functional Maps on Landmark-Adapted Bases (CGF) |
CURVES & FEATURES chaired by Jorg Peters
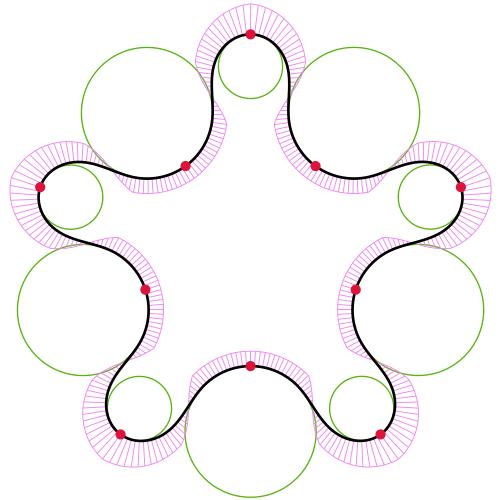
|
Smooth Interpolating Curves with Local Control and Monotone Alternating Curvature |

|
b/Surf: Interactive Bézier Splines on Surface Meshes (TVCG) |

|
SGLBP: Subgraph-based Local Binary Patterns for Feature Extraction on Point Clouds (CGF) |
LEARNING & CREATING chaired by Julie Digne

|
PriFit: Learning to Fit Primitives Improves Few Shot Point Cloud Segmentation |

|
SDF-StyleGAN: Implicit SDF-Based StyleGAN for 3D Shape Generation |
|
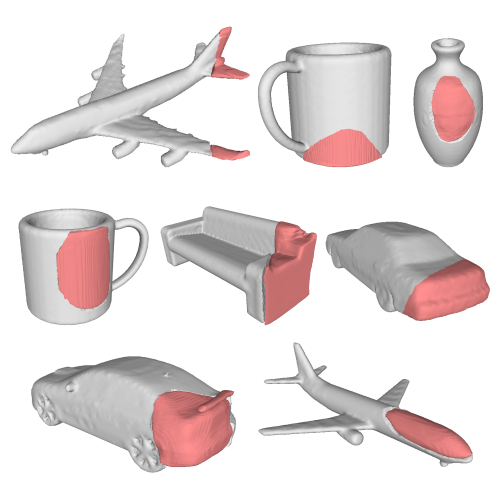
MendNet: Restoration of Fractured Shapes Using Learned Occupancy Functions |
MESHES & PARTITIONS chaired by David Bommes
|
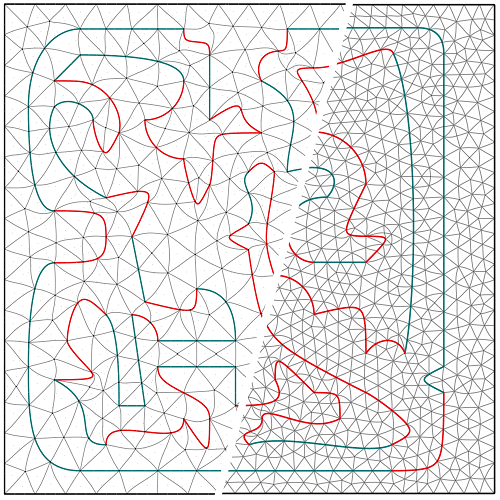
Precise High-order Meshing of 2D Domains with Rational Bézier Curves |
|
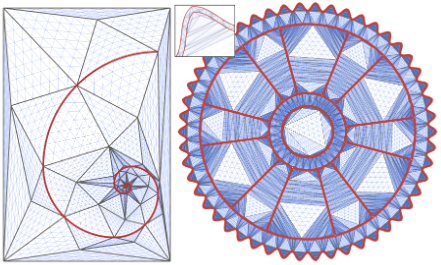
Rational Bézier Guarding |
|
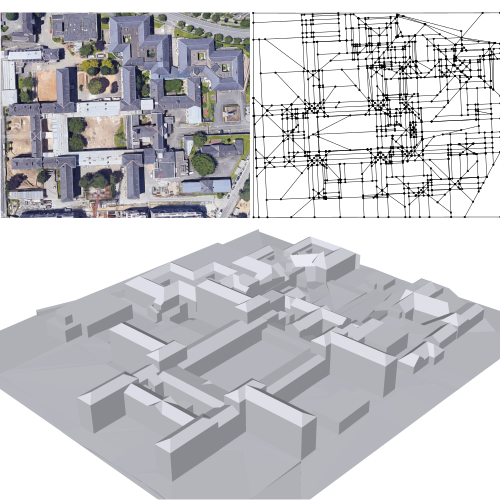
Simplification of 2D Polygonal Partitions via Point-line Projective Duality, and Application to Urban Reconstruction (CGF) |
TOOLS & DATA chaired by Justin Solomon

|
Deterministic Linear Time for Maximal Poisson-Disk Sampling using Chocks without Rejection or Approximation |

|
TinyAD: Automatic Differentiation in Geometry Processing Made Simple |

|
Hex Me If You Can |
TILING & NESTING chaired by Pierre Alliez

|
Constructing L∞ Voronoi Diagrams in 2D and 3D |

|
Fabricable Multi-Scale Wang Tiles |
|
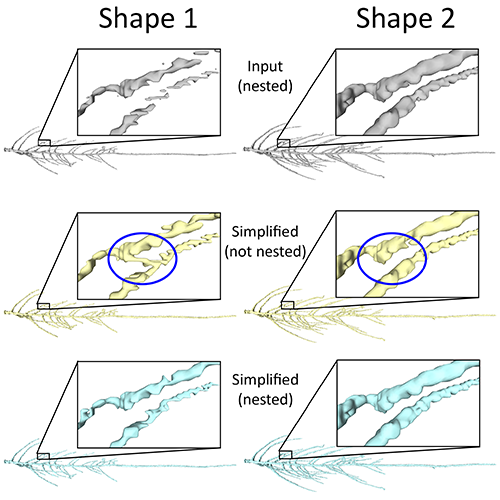
Topological Simplification of Nested Shapes |
The detailed Conference Program Schedule is available as PDF.
(The file with timestamp 2022-06-20 09:00:00 is the current one)
